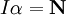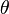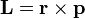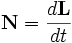STLファイルフォーマット からスクラップ:
バイナリフォーマット
* 構文
バイト数 データ型 データ内容
80 char[ ] 任意の文字列
4 unsigned int 三角形の枚数
- - 1つ目の三角形データ
4 float 三角形の法線ベクトルのX成分値
4 float 三角形の法線ベクトルのY成分値
4 float 三角形の法線ベクトルのZ成分値
4 float 三角形の1点目の頂点のX座標値
4 float 三角形の1点目の頂点のY座標値
4 float 三角形の1点目の頂点のZ座標値
4 float 三角形の2点目の頂点のX座標値
4 float 三角形の2点目の頂点のY座標値
4 float 三角形の2点目の頂点のZ座標値
4 float 三角形の3点目の頂点のX座標値
4 float 三角形の3点目の頂点のY座標値
4 float 三角形の3点目の頂点のZ座標値
2 - 未使用データ
- - 2つ目の三角形データ
4 float 三角形の法線ベクトルのX成分値
4 float 三角形の法線ベクトルのY成分値
4 float 三角形の法線ベクトルのZ成分値
4 float 三角形の1点目の頂点のX座標値
4 float 三角形の1点目の頂点のY座標値
4 float 三角形の1点目の頂点のZ座標値
4 float 三角形の2点目の頂点のX座標値
4 float 三角形の2点目の頂点のY座標値
4 float 三角形の2点目の頂点のZ座標値
4 float 三角形の3点目の頂点のX座標値
4 float 三角形の3点目の頂点のY座標値
4 float 三角形の3点目の頂点のZ座標値
2 - 未使用データ
・・・ - (三角形の法線ベクトルのX成分値から未使用データまでを1枚の三角形データとして三角形枚数分のデータが続く)
VC で C言語、C++互換で書くと、こんな感じかな。
typedef struct tagSTL_FILE_HEADER
{
char comment[80]; // オブジェクト名
unsigned int numberOfTriangles; // トライアングル数
} STL_FILE_HEADER, *LP_STL_FILE_HEADER;
#pragma pack(push,1)
typedef struct tagSTL_TRIANGLE_ENTRY
{
float n[3]; // 三角形の法線ベクトルのXYZ成分値
float v1[3]; // 三角形の1点目の頂点のXYZ座標値
float v2[3]; // 三角形の2点目の頂点のXYZ座標値
float v3[3]; // 三角形の3点目の頂点のXYZ座標値
unsigned short reserved; // 未使用データ
} STL_TRIANGLE_ENTRY, *LP_STL_TRIANGLE_ENTRYR;
#pragma pack(pop)
構造体のアラインメントを正しくセットしないと、読んでいくうちにずれちゃう。
この場合は、ズレを考慮して1トライアングルづつ読み込む事も不可能ではないけど、
ディスクアクセスの効率を考えたら、動的メモリ確保で作った配列を使用して、
まとめ読みした方が確実に早いので、その場合は、アラインメントの調整は必須。
(その分メモリを多く要するけど、最近はメモリがたくさん載っている事が多いから、、、)









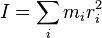

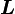 と角速度
と角速度 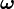 の関係は
の関係は


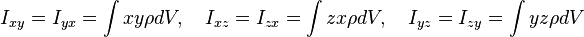
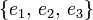 をえらぶことで
をえらぶことで のことを主慣性モーメントと呼ぶ。慣性主軸座標系では角運動量は
のことを主慣性モーメントと呼ぶ。慣性主軸座標系では角運動量は

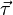 と位置ベクトル
と位置ベクトル 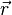 と力
と力 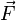 との関係(上の式)、および運動量のモーメント(角運動量)
との関係(上の式)、および運動量のモーメント(角運動量) と位置ベクトル
と位置ベクトル 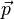 との関係(下の式)。
との関係(下の式)。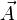 との
との を、O 点まわりの
を、O 点まわりの  とすると、混合3重積
とすると、混合3重積 で表される。こちらは
で表される。こちらは と記述される。ここで、もし
と記述される。ここで、もし  は
は